I like tofu. I especially like well browned, pan fried tofu.

The issue is, cooking pan fried tofu can be a pain. The way my mom does it, she puts lets the tofu sit for two-three minutes on each side, then meticulously rotates each one onto a fresh side. She then repeats the process for at least four of the six sides.

I’m perfectly fine with her process, as long as she’s the one cooking (I’m a horrible son), but every other day or so, I like to assuage my guilt by helping out with dinner. Yesterday, that meant I was in charge of the tofu. I’d seen my mom cook tofu before, and wasn’t about to let altruism get in the way of my laziness. I decided to do what my wise CS professor once told his lecture of one hundred impressionable freshmen. Sometimes you just gotta flip a coin (though I think he was trying to tell us to take leaps of faith, no cooking advice intended).

In my case, much to Mother’s chagrin, I decided to flip the tofu. Every minute or so, I randomly tossed the tofu, and hoped for the best.

That got the probability nerd in me thinking…

The question

What is the optimal, randomized, way to pan fry tofu? That is, how long should I let the tofu fry on a side before tossing it to minimize the time it takes before 90% of the tofu squares has four or more well browned sides?

My assumptions/parameters:

  • My tofu flipping is uniformly and independently random
  • Each flip costs 0.1 minutes of cooking time (to account for flipping time + cooling effect, and because \(\frac{1}{10}\) is a nice number)
  • The time for ideal browning seems to be somewhere around 2-2.5 minutes on a side. For my purposes, I set 2 minutes as the minimum for a well-browned tofu face

Defining the problem

First let me define some variables. \[ \begin{split} T :=& \text{ total cooking time}\newline t :=& \text{ time per flip}\newline k :=& \text{ flips per 2 minutes}= \frac{2}{t}\newline n :=& \text{ number of flips}\newline\newline X_{k,n} :=& \text{ number of browned faces for a given tofu after toss }n \newline & \text{ parametrized by }k\newline \end{split} \] We’re trying to minimize \[ \begin{equation}\label{eq:T} T=(t+0.1)n=(\frac{2}{k}+0.1)n \end{equation} \] Going in, my first hope was to be able to come up with a close form expression for \(n\) in terms of \(k\). Then optimizing would be as simple as taking the derivative with respect to \(k\) of \(T\).

The \(n\) we need is one such that: \[ \begin{equation} P(X_{k, n}\geq 4)\geq 0.9 \end{equation}\] In other words, the number of flips required to ensure that the probability of the number of browned faces being at least 4 is at least 90%.

Solution setup

OF COURSE my first step was to define the sample space (I hope you’re proud Professor Venkatesh). Since we’re looking just at one given tofu, the sample space is the sequence of face down faces. To make the question feel more familiar for myself, I analogized it to the probabilist’s second favorite setting (behind the holy coin toss): think of it as a sequence of tosses of a die, where each face of the tofu is assigned a number from 1 through 6. In notation: \[\Omega=\{r_1r_2\dots r_n : r_i\in 1\dots 6\}\] The event in question is then the subset of \(\Omega\) for which we can partition the \(r_i\)s into six sets by side number, where a minimum of four of the sets have size at least \(k\). That’s quite a mouthful. So the three pounds of junk between my ears decided to simplify.

What if we broke up \(X_{k, n}\geq 4\) into \(X_{k, n}= 4\), \(X_{k, n}= 5\), and \(X_{k, n}= 6\)? What if we then went even further and define \(Y_{k,n}^m\) as the event that the first \(m\) sides (sides 1 through \(m\)) appear at least \(k\) times. So for example, [1,1,1,2,2,3,3,3] and [6,5,3,3,2,2,1,1] would be members of \(Y_{2,8}^3\), while [4,4,5,5,5,6,6,6] and [1,2,2,3,3,3,3,3] would not.

We can then define the original event as \[ [X_{k,n}\geq 4] = [X_{k, n}= 4] \cup [X_{k, n}= 5] \cup [X_{k, n}= 6] \] Where the events are mutually disjoint, so that by Kolmogrov’s third axiom: \[ \begin{equation}\label{eq:PX_geq} P[X_{k,n}\geq 4] = P[X_{k, n}= 4] + P[X_{k, n}= 5] + P[X_{k, n}= 6] \end{equation} \] Because the event \(Y_{k,n}^m\) generalizes to any set of \(m\) sides, and there are \({6\choose m}\) such sets: \[ \begin{equation}\label{eq:PX_eq} |X_{k, n}= m| = {6\choose m} |Y_{k,n}^m| \implies P[X_{k, n}= m] = {6\choose m} P[Y_{k,n}^m] \end{equation}\]

\([Y_{k,n}^m]\) can be generated by:

  1. first finding a multiset \( S_m= \{1\times s_1, 2\times s_2, 3\times s_3, 4\times s_4, 5\times s_5, 6\times s_6 \}\), where \(s_i\) is the number of times face \(i\) appears, with the constraints: \[ \begin{split} \sum_{i=1}^6 s_i &= n \newline s_i & \geq k \quad \forall i\in [1\dots m] \newline s_i & < k \quad \forall i\in [m+1 \dots 6] \end{split} \]
  2. then finding all the permutations of said multiset \(S\)

We can then calculate the probability of \([Y_{k,n}^m]\) as: \[ \begin{equation}\label{eq:PY} P[Y_{k,n}^m]=\frac{\sum_{\forall S_m} |p(S_m)|}{6^n} \end{equation} \] Where \(p(\cdot)\) is the function from multisets to the set of permutations of a multiset.

Step 1

A brief trip down a dead end road

My first instinct for solving step 1 was to use stars and bars, “initializing” the first \(m\) faces with \(k\) flips each; i.e. stars and bars with \(n-mk\) stars and \(6-1\) bars. The problem is, though, that in addition to the lower bound of \(k\) for the first \(m\) faces, there’s also an upper bound for the last \(6-m\) faces. We defined the event as exactly \(m\) of the faces showed up a minimum of \(k\) times. That means the other faces must show up less than \(k\) times.

I hate to make assumptions, but if you’re at all like me, you might be thinking, why don’t we scrap this notion of equality and instead keep the event as greater than or equal? That way we wouldn’t have to worry about any upper bounding. We would once again “initialize” \(m\) faces with \(k\) flips, and just proceed with stars and bars. That’s what I hoped, but unfortunately, the devil (a.k.a double counting) stops us. Consider this example. Setting the parameters as \(k=1,n=6,m=4\), the multiset where all the faces occur once would be counted in all \({6 \choose 4}\) of the choices of the four initialized faces.

Abandonment of closed form

By now, I’d realized that I wasn’t going to find a closed form solution to the problem. Even if I somehow fixed the upper bound problem above, steps 1 and 2 are not independent of each other, so the multiplication rule would not apply. So I turned to the next best thing: Python.

from functools import reduce
from math import factorial, inf, comb, pow
from typing import List
import pandas as pd

memo = [[[[[] for m in range(6 + 1)] for k in range(30)] for j in range(100)] for length in range(6 + 1)]

# Generates the multisets for a given length, number of flips (n), flips to brown (k), and number of faces (m)
def generate_multisets_helper(length: int, k: int, n: int, m: int) -> List[List[int]]:
    # base case
    if length == 1:
        if (m > 0 and n >= k) or (m == 0 and n < k):
            memo[length][n][k][m] = [[n]]
            return memo[length][n][k][m]
        # if conditions aren't satisfied, then there's no possible such multiset
        return []

    # memoization
    if len(memo[length][n][k][m]) > 0:
        return memo[length][n][k][m]

    adder = 0 if m == 0 else k # add k if this is one of the first m faces
    maxi = min(n + 1, k if m == 0 else inf) # upper bound
    multisets = []
    for i in range(adder, maxi):
        next_res = generate_multisets_helper(length - 1, k, n - i, max(m - 1, 0))

        current = list(map(lambda ms: ms + [i], next_res))
        multisets.extend(current)

    memo[length][n][k][m] = multisets
    return multisets


def generate_multisets(k: int, n: int, m: int):
    return generate_multisets_helper(6, k, n, m)

What the function above does is, for each possible number of flips, say \(i\), assignable to face 1, calculates the possible multisets for the rest of the faces (by recursively calling the function with length - 1, n - 1, and m - 1) and tacks on \(i\) as the number of occurrences of case 1 for each of the possible multisets.

Step 2

The next step is to calculate the number of possible permutations for each multiset. This is found by calculating all permutations of length \(n\), then dividing by the number of permutations of the appearances of each face to eliminate double counting: \[\frac{n!}{s_1!s_2!s_3!s_4!s_5!s_6!}\]

def multiset_perms(multiset: list):
    numerator = factorial(sum(multiset))
    denominator = reduce(lambda acc, x: acc * factorial(x), multiset, 1)
    return numerator/denominator

Working backwards

The rest of it is plug and chug, working backwords from the probability of \(Y_{k,n}^m\) to \(X_{k,n}=m\) finally to \(X_{k,n}\geq m\) by applying equations \(\ref{eq:PY}\), \(\ref{eq:PX_eq}\), and \(\ref{eq:PX_geq}\) in that order.

def prob_Y(k: int, n: int, m: int):
    multisets = generate_multisets(k, n, m)

    size_Y = reduce(lambda acc, ms: acc + multiset_perms(ms), multisets, 0)  # size of event Y_{k,n}^m
    size_omega = pow(6, n) # size of the sample space

    return size_Y / size_omega


def prob_X_equals_m(k: int, n: int, m: int):
    combs = comb(6, m)

    return combs * prob_Y(k, n, m)


def prob_X_atleast_m(n: int, k: int, m: int):
    return sum(map(lambda i: prob_X_equals_m(k, n, i), range(m, 6 + 1)))

Optimization

By now, we’ve made our way backwards from multiset permutations all the way to the probability of the original event in question, \(X_{k,n}\geq m\). It remains to find the optimal \(k\); the \(k\) which minimizes time T from equation \(\ref{eq:T}\). Since no close form expression emerged, my plan was to:

  1. calculate the number of flips required for a certain confidence level, 
    def flips_required_for_confidence(confidence: float, k: int, m: int):
 current_conf = 0
 n = 1
 while current_conf < confidence:
     current_conf = prob_X_atleast_m(n, k, m)
     n += 1
 return n
  2. plug that into \(\ref{eq:T}\) to calculate time required, and 
    def total_time_required_for_confidence(flip_time: float, brown_time: float, confidence: float, n: int, m: int):
 return (brown_time / n + flip_time) * flips_required_for_confidence(confidence, n, m)
  3. plot the times for different choices of \(k\). 
    def times_required_dataframe(flip_time: float, brown_time: float, confidence: float, m: int, top: int):
 ran = range(1, top)

 ks = pd.Series(ran, name="K")
 times = pd.Series(map(lambda k: total_time_required_for_confidence(flip_time, brown_time, confidence, k, m),
                       ran), name="Times")

 return pd.concat([ks, times], 1)

Results

To experiment with the optimization, I used the following Jupyter notebook:

tofu
In [1]:
from tofu import total_time_required_for_confidence, flips_required_for_confidence, times_required_dataframe, prob_X_atleast_m
import tofu
import pandas as pd
import matplotlib.pyplot as plt
In [2]:
FLIPS_COL_NAME = "Flips"
PROBS_COL_NAME = "Probabilities"

# First I wanted to take a look at the function from flips -> probability
def generate_probs_dataframe(k: int, m: int, top: int, step: int):
    ran = range(1, top, step)

    flips = pd.Series(ran, name=FLIPS_COL_NAME)
    probs = pd.Series(map(lambda n: prob_X_atleast_m(n, k, m), range(1, top, step)), name=PROBS_COL_NAME)

    return pd.concat([flips, probs], 1)

df = generate_probs_dataframe(2, 4, 25, 1) # 1 minute between flips, 4 browned sides

df.plot(FLIPS_COL_NAME, PROBS_COL_NAME)
Out[2]:
<matplotlib.axes._subplots.AxesSubplot at 0x11bacc190>
In [3]:
# The graph looks like a sigmoid function whose slope increases rapidly, and decreases slowly
# Is there a closed form function with this shape?
In [4]:
# NOW..... to optimize
In [5]:
df = times_required_dataframe(0.1, 2, 0.90, 4, 6)
df.plot("K", "Times")
Out[5]:
<matplotlib.axes._subplots.AxesSubplot at 0x11cf883a0>
In [6]:
total_time_required_for_confidence(0.1, 2, 0.90, 3,4) # time in the optimal case
Out[6]:
18.4
In [7]:
flips_required_for_confidence(0.90, 3, 4) # number of flips in the optimal case
Out[7]:
24
In [8]:
# I wanted to see what happens with different confidence and face count targets

conf_levels = [0.5, 0.6, 0.7, 0.8, 0.9, 0.95]
face_counts = [3,4,5]

fig, axs = plt.subplots(len(conf_levels), len(face_counts), figsize=(12, 24), sharex='col')
# plot plots
for i in range(0, len(conf_levels)):
    for j in range(0, len(face_counts)):
        conf_level = conf_levels[i]
        face_count = face_counts[j]
        df = times_required_dataframe(0.1, 2, conf_level, face_count, 9)
        df.plot("K", "Times", ax=axs[i, j])
        axs[i, j].set_title("(Conf={}%, m={})".format(conf_level*100, face_count))

plt.show()

And the winner is…

K=3! (at least for a target of 90% with four browned sides) with a total cook time of 18.4 minutes with 24 flips. 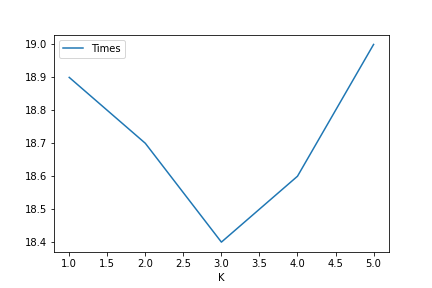Plot for 4 sides at a confidence of 90% Graph from line [5] in the jupyter notebook

Observations

  • Higher confidence level (more successful tofu squares in expectation) means higher optimal \(k\)
  • Higher target number of browned faces means higher optimal \(k\)
  • As should be expected, higher conf and m means higher ovearll cooking time
  • In the case of \(m=3\), it’s almost always optimal to leave the tofu for 2 minutes on a side (only exception is the 95% confidence case)
  • The graphs look weirdly un-smooth. Just an effect of rounding errors?

Questions for further exploration

This is all well and good, but I’m ignoring another important feature of well-browned tofu. It’s not over done.

  • What is the mean and variance in the optimal case I found?
  • What is the smallest value of \(k\) that allows us to hit a mean and variance target (say 4 brown sides with no more than 80% with less than 3 or more than 5)?

Maybe I’ll look into these questions at some point. Before that, though, I’m going to test out my results…

Update (07-18):

I finally got around to testing out my method and….. the results were mixed. The tofu turned out fine, actually really good. The sides were all, pretty uniformly, well browned. Some nice looking tofu But turns out flipping every 46 seconds (40 + 6 to incorporate the flip time), 24 times in a row for a total of 18 minutes can… be a little tiring. I did notice that most of the sides were more browned them I’m used to. This makes sense, since the expected value of time on a side is \(\frac{2}{k}*24/6 = \frac{8}{3} \approx 2.67\) minutes.

Now I wonder what happens if I set my targets a little lower, and optimize for minimum number of flips. What is the minimum number of flips required to get an expected value of 2 minutes on each side while also keeping variance low. Perhaps with a standard deviation within 20 seconds.